Sommaire

Introduction

Pour la plupart des gens, le chemin le plus rapide pour aller d'un point à un autre est la ligne droite. Nous allons vous montrer que les idées reçues sont fausses. Le but de ce T.I.P.E. est de vous montrer ce qu'il en est réellement.

En effet, l’un des problèmes les plus connus de l’histoire des mathématiques est le problème brachistochrone: trouver la courbe le long de laquelle une particule glisserait d’un point à un autre en un minimum de temps en étant soumis à un champ uniforme de pesanteur. Ce problème a été posé par Jean Bernoulli en 1696 comme un challenge pour les mathématiciens de son époque. La solution fut trouvée par Jean Bernoulli lui-même ainsi que par son frère Jacques Bernoulli, Newton, Leibniz et le marquis de l’Hospital. Le problème brachistochrone est important dans le développement des mathématiques et s'avère être une des applications principales de la méthode du calcul des variations.

I Calcul des variations

L’étude d’une fonction à valeurs réelles comporte en particulier la détermination de ses extremums. C’est là un des objets du calcul différentiel classique lorsque la source de cette fonction est un espace numérique ; c’est l’objet de ce qu’Euler a appelé le calcul des variations lorsque cette source est un espace fonctionnel.

On rencontre déjà dans la plus haute antiquité des problèmes d’une telle nature. La légende ne veut-elle pas que Didon, lorsqu’elle fonda Carthage, ait délimité la plus grande étendue qu’elle pût circonscrire à l’aide de lanières découpées dans la peau d’un taureau ? Et il est bien connu que les Grecs caractérisaient un segment de droite comme la ligne de plus petite longueur joignant ses extrémités.

Ce n’est cependant qu’au XVIIIe siècle, à la suite de l’essor du calcul infinitésimal, qu’Euler et Lagrange établirent les fondements du calcul des variations et donnèrent une première condition d’extremum. Cette équation d’Euler-Lagrange allait jouer un rôle très important, surtout en physique, où elle justifiait les principes variationnels : principe de Fermat (appliqué dans la deuxième partie de ce devoir) pour la propagation de la lumière dans les milieux différemment réfringents; principes de moindre action de Maupertuis et Hamilton pour la détermination des mouvements en mécanique analytique.

La recherche de conditions d’extremum se poursuivit aux XVIIIe et XIXe siècles, notamment avec les travaux de Legendre, Jacobi et Weierstrass, pour aboutir au début du XXe siècle à une théorie bien élaborée que l’on situe aujourd’hui dans le cadre du calcul différentiel au sens de Fréchet dans les espaces de Banach. Mais de difficiles problèmes relatifs à l’existence de ces extremums restent encore ouverts.

Plus récemment, les travaux de Morse relancèrent l’intérêt porté au calcul des variations. Utilisant à la fois des techniques d’analyse fonctionnelle, de topologie algébrique et de topologie différentielle, ils sont à l’origine de ce qu’on appelle maintenant l’analyse différentielle globale, une des théories carrefours de la mathématique actuelle.

Lorsqu’on cherche les valeurs extrémales d’une fonction f d’une variable x, c’est à dire lorsqu’on cherche les valeurs de la variable x pour lesquelles la valeur f(x) est maximale ou minimale, on regarde en quels points la représentation graphique de f admet une tangente horizontale, autrement dit on cherche les valeurs de x pour lesquelles f’(x)=0. Dans le cas d’une fonction f de 2 variables x et y, on est amené à considérer les points en lesquels le plan tangent à la surface d’équation z=f(x, y) est horizontal, autrement dit on cherche les couples (x, y) pour lesquels les dérivées partielles par rapport à x et à y sont nulles. On dit aussi qu’en ces points la fonction f est stationnaire. Par exemple, dans le cas de la fonction altitude à la surface terrestre, les plans tangents horizontaux correspondent aux sommets, aux puits et aux cols, traduction en 2 variables des maxima, minima et points d’inflexion. Bref, dans le cas d’un nombre fini de variables, les difficultés paraissent surmontables, l’approche du problème s’effectuant à l’aide du Calcul Différentiel de Newton et Leibniz.

Ici ce qui varie n’est plus un nombre ou un point, mais une courbe, une fonction, et ce qu’il convient de minimiser ou de maximaliser est un nombre dépendant de cette courbe ou de cette fonction. Il faut imaginer une nouvelle théorie, une extension du Calcul Différentiel. Cette théorie à créer s’appelle le Calcul des Variations, les variations étant celles d’une fonction. Mais, en 1696, cette théorie n’est pas encore fondée et notre problème s’avère a priori d’un abord délicat.

On considère dans le champ de la pesanteur deux points A et B et un point matériel M se déplaçant sans frottement sur une courbe d’extrémités A et B. Déterminer la courbe, appelée brachistochrone, pour laquelle le temps de parcours est minimal lorsque le point M part du point A avec une vitesse nulle. La quantité à extrémiser, (ici le temps de parcours) s’exprime généralement sous la forme d’une intégrale :

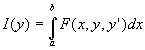
où y désigne la fonction à trouver, y’ sa dérivée, x la variable, F une certaine fonction.

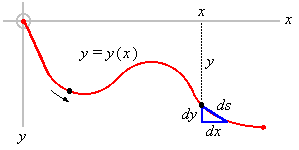
A l’abscisse x sur le graphe, l’énergie potentielle perdue est mgy, équivalente à l’énergie cinétique acquise par le point matériel depuis le départ.

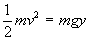
D’où :

NB : On aurait pu remplacer les notations y et v par y(x) et v(x) étant donné que ces variables sont bien sûr liées à la coordonnée horizontale x.

La vitesse v est mesurée le long de la courbe si bien que nous devons réécrire l’expression en composantes horizontales et verticales

• s représente l’abscisse curviligne
• ds représente l’accroissement de cette distance le long de la courbe
• dx et dy représentent les composantes horizontales et verticales de ds

Ainsi,

• ds/dt représente la vitesse le long de la courbe
• dx/dt représente la composante x de la vitesse
• dx et dy sont données par le théorème de Pythagore

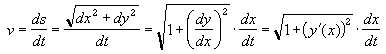
En insérant l’équation obtenue d’après les principes de la dynamique

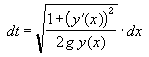
Une simple intégration nous donne l’expression de t :

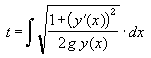
Il s’agit maintenant de trouver le minimum atteint par t parmi toutes les fonctions y(x) satisfaisant :

• y(x=0)=0, y(x=a)=b

Le problème fondamental du calcul des variations consiste à chercher, parmi les fonctions y=f(x) continûment dérivables sur un intervalle donné [a,b] et pour lesquelles les fonctions f(a) et f(b) sont des valeurs données, celles qui rendent maximum ou minimum l’intégrale précédente.

Pour appliquer cette méthode, on part de l’équation d’Euler-Lagrange :

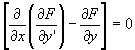
qui donne les extremums de l'intégrale :

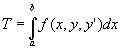
On peut alors utiliser l'identité de Beltrami:

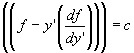
Dans notre cas :

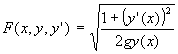
Donc

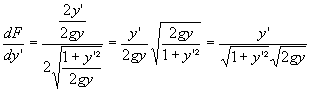
En remplaçant dans l'équation différentielle, on trouve:

II Méthode de Jean Bernoulli

La méthode de Jean Bernoulli est basée sur un principe simple: celui de la lumière. En effet: pour aller d'un point à un autre, la lumière emprunte toujours le chemin le plus court. Dans le programme de Spé de physique, seul un aspect simple du problème est abordé: celui où la vitesse de la lumière est constante, c'est à dire qu'on a une propagation dans un milieu d'indice constant donc une propagation rectiligne. Si on imagine que la vitesse de la lumière varie de la même façon que la vitesse d'une particule qui glisse le long d'une courbe, on se ramène au problème de Brachistochrone. Jean Bernoulli expose sa démonstration dans les Acta Eridutorum de mai 1697. Sa méthode correspond typiquement à ce que nous appelons maintenant une discrétisation du problème. Il imagine l'espace découpé en fines lamelles, lesquelles étant suffisamment fines de manière à pouvoir considérer la vitesse constante à l'intérieur de chacune. Dans chaque bande, la trajectoire (devant être le plus court chemin) est nécessairement un segment. Globalement, la trajectoire présente alors l'allure d'une ligne polygonale.

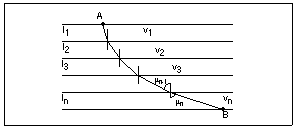
Le plus difficile maintenant est d'imaginer comment s'effectue le passage d'une bande à la bande suivante. Pour cela, il suffit de ramener ce problème à celui de la propagation de la lumière. Appelons v_i la vitesse dans une certaine bande, v_r celle dans la bande juste en dessous; i et r les angles d'incidence et de réfraction ainsi que n_i et n_r les indices des milieux d'incidence et de réfraction. D'après les lois de DESCARTES, on sait que n_i.sin(i) = n_r.sin(r). De plus, pour la réfraction, on sait que la vitesse de la lumière est égale au quotient de c (qui à la même valeur dans chaque bande) par l'indice du milieu traversé.

On peut donc en déduire la relation suivante:

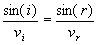
Si l'on imagine maintenant que les lamelles horizontales deviennent de plus en plus fines, leur nombre augmentant indéfiniment, la ligne polygonale tend vers une courbe. La tangente en chaque point de cette courbe se confond en ce point avec le segment de la ligne polygonale. L'angle u que fait la tangente avec la verticale est donc lié à la vitesse v par la relation suivante:

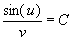où C est une constante.

Ici, la vitesse résulte de l'action de la pesanteur et comme nous le savons d'après Galilée, elle est fonction de la hauteur de chute y selon la formule :

On est donc ramené à résoudre l'équation suivante:

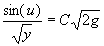
Nous allons maintenant essayer de ramener la précédente équation à une équation différentielle. Tout d'abord, on peut remarquer d'après le schéma que :

De plus, en sachant que :

On peut démontrer très facilement que :

L'équation trouvée précédemment peut se transformer ainsi

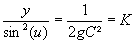
A l'aide des indications démontrées plus haut, on est donc ramené à l'équation différentielle suivante:

On peut donc voir que le problème brachistochrone, quelle que soit la méthode utilisée pour le résoudre, aboutit sur la même équation différentielle.

Celle-ci étant par ailleurs très difficile à résoudre, nous avons décidé de consacrer une partie entière à la résolution de cette équation.

III Résolution du problème avec Maple

Le but de cette résolution est de trouver une solution à l'équation différentielle suivante:

Ce qui revient à résoudre l'équation suivante à une "translation" près:

Nous allons donc résoudre ce problème avec Maple.

Nous faisons d’abord un alias pour y' pour rendre le calcul plus facile. Nous faisons aussi les suppositions nécessaires sur nos variables.

> restart:

> alias(`y'`=yp):

> assume(c>0,x>0,y>0,y1>0,y<y1):

> f:=(1+yp^2)^(1/2)/(y1-y)^(1/2);

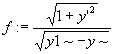
On applique le principe variationnel vu précédemment.

> normal(f-yp*diff(f,yp))=c;

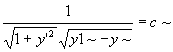
On résout maintenant pour y'.

> solve(%,yp);

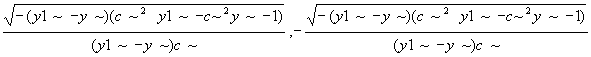
Nous trouvons ainsi toutes les possibilités pour notre solution (et même une solution en trop). "c" est une des deux constantes d’intégration qui sont déterminées par les points de départ et d’arrivée (0,0) et (x1,y1). Pour faciliter le problème on prendra c=1 et y1=1.

> sols:=[%]:

> subs(c=1,y1=1, sols);

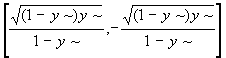
> expand(radical(%[2]));

On a besoin de suppositions sur y et x.

> y:='y': x:='x':

Nous avons maintenant l’équation différentielle qu’il faut résoudre.

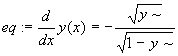
> ans:=dsolve( eq, y(x) );

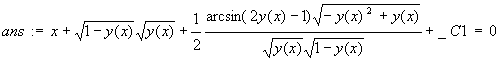
On peut la simplifier sous une meilleur forme.

> map(combine,lhs(ans)-_C1, radical, symbolic);

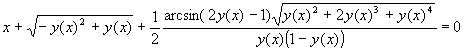
Comme 0<y(x)<1 et y(x)^2 > y(x) , ce qui signifie que sqrt(y(x)^2-2*y(x)^3+y(x)^4) =y(x)*sqrt(1-2*y(x)+y(x)^2) = y(x)*(1-y(x)), ce qui fait une belle simplification.

Notre réponse simplifiée est donc :

> ans:=x+sqrt(y(x))*sqrt(1-y(x))+1/2*arcsin(2*y(x)-1)=_C1;

On obtient une solution de la forme f(y)=x. On peut la simplifier en une solution paramétrique, comme "y" va de 0 à y1, on définit "t" de la façon suivante :

> Y:=(y1/2)*(1-cos(t)):

> Y:=subs(y1=1,Y);

Il s’agit de notre équation paramétrique pour "y" et celle pour "x" est déterminée par:

> normal(subs(y(x)=Y,ans));

> subs(cos(t)^2=1-sin(t)^2,%);

> simplify(expand(radical(%)));

> X:=solve(%,x);

Si on reprend les conditions initiales pour (x,y) de manière à avoir t=0 en (0,0).

> _C1:=solve(subs(t=0,X),_C1):

Nous avons notre équation paramétrique finale :

> x=X; y=Y;

ce qui forme une cycloïde comme on peut le voir ci dessous:

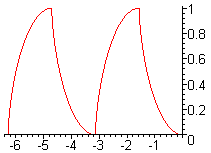> plot([X,Y,t=0..4*Pi]);

A l'aide de MAPLE, on arrive donc à montrer que le chemin le plus rapide pour aller d'un point à un autre est une portion de cycloïde. Il faut donc conseiller aux skieurs lorsqu'ils parcourent un slalom de suivre un arc de cycloïde pour gagner du temps...

IV Propriétés de la cycloïde

Cette cycloïde, qui on vient de le démontrer, est une courbe brachistochrone, est aussi, on le savait avec Huygens depuis 1659, une courbe tautochrone : les corps qui tombent dans une cycloïde renversée arrivent au point le plus bas dans le même temps, de quelque hauteur qu’ils commencent à tomber.

Huygens a aussi construit la première horloge dans le but de montrer que le pendule était isochrone en le forçant à osciller en arc de cycloïde. L’expérience est réalisée en plaçant deux développées d’arcs de cycloïde inversée(retournée) de chaque côté du point de suspension du pendule contre lesquels le pendule est contraint de se déplacer. Malheureusement, les frottements expérimentaux le long des arcs cause une plus grosse erreur que celle corrigée par le chemin cycloïdal.

Les équations paramétriques de la cycloïde sont :

Pour montrer que la cycloïde satisfait la propriété tautochrone, on considère les dérivées :

Ainsi,

La conservation d’énergie..

..s’écrit donc :

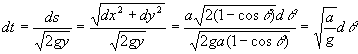
Donc le temps requis pour aller du haut au bas de la cycloïde est :

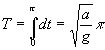
Cette durée ne dépend donc que de paramètres constants.

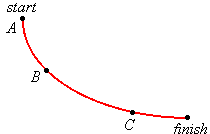
A, B et C, partant au même moment, arriveront ainsi dans le même temps.

Conclusion

L'énoncé en1696 du problème brachistochrone peut être considéré comme l'authentique acte de naissance du calcul des variations, car c'est ce problème qui suscite la recherche de méthodes générales progressivement élaborées au cours d'une véritable compétition.

Cette étude nous a permis d'approfondir plusieurs parties du programme de spé, comme le principe de Fermat, les intégrales à plusieurs variables, les dérivées partielles, les problèmes d'extremums d'intégrales et enfin d'utiliser Maple.