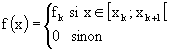 .
.Compression d’images
par ondelettes
par Rémi Pauchet et Damien Velleman
Introduction
*I/ La théorie des ondelettes
*1) les ondelettes de Haar
*2) algorithme de calcul des coefficients des ondelettes de Haar
*II/ Compression d'un signal
*1) Approximation d'un signal
*2) décomposition du signal sans pertes
*3) Décomposition d’un signal avec pertes
*III/ Compression d'une image
*1) Présentation de l’algorithme
*2) Schéma de l’algorithme
*3) Exemples d’images compressées par ondelettes
*Conclusion
*Bibliographie
*Annexes
*1) Programme Compress
*2) Programme decompress
*3) Applet compression d’un signal
*Dans l’histoire des mathématiques, les séries de fourrier ont marqué une avancée considérable en permettant d’approximer des signaux périodiques par une somme de sinus et de cosinus. En 1909 Haar, avec les fonctions portant son nom, a défini ce que l’on peut considérer comme les premières ondelettes. L'analyse de Fourier permet de caractériser la régularité globale d'une fonction, la transformée en ondelettes permet d'analyser la régularité ponctuelle d'une fonction. La transformée par ondelettes est la décomposition d'un signal par une ondelette mère qui sera translatée et dilatée.
L’utilisation des ondelettes de Harr permet, entre autres utilisations, la compression de signaux et d’images. Ce que nous allons développer dans ce TIPE.
Une transformation par ondelettes consiste à décomposer un signal en une tendance grossière accompagnée de détails de plus en plus fins. Ainsi, pour reconstituer le signal avec une précision donnée, il suffira de connaître la tendance et les détails correspondant au niveau de précision recherché et de négliger les autres.
Considérons un signal échantillonné régulièrement sur [0;1] en 2P
points, on note ces points ![]()
![]() . On associe à cet échantillon une fonction f définie
par :
. On associe à cet échantillon une fonction f définie
par : 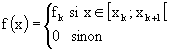 .
.
Quand cet échantillonnage varie, la fonction f décrit l'ensemble Ep
des fonctions constantes sur chacun des intervalles ![]() ,
, ![]() et nulles en dehors de
l'intervalle
et nulles en dehors de
l'intervalle ![]() .
.
Ep est un sous-espace vectoriel de l'espace vectoriel des
fonctions réelles à valeurs réelles. De plus, quand on fait varier p, les espaces Ep
sont emboîtés, c'est à dire que ![]() . Leur réunion
est donc encore un sous-espace vectoriel E de l'espace vectoriel des fonctions réelles à
valeurs réelles.
. Leur réunion
est donc encore un sous-espace vectoriel E de l'espace vectoriel des fonctions réelles à
valeurs réelles.
On munit l'espace vectoriel E du produit scalaire définit par : 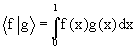 .
.
Pour obtenir une base de Ep, il suffit de considérer les
fonctions ![]() définies par
définies par 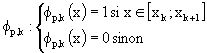 .
.
En effet, par définition même de Ep, toute fonction f de Ep
se décompose de façon unique sous la forme ![]() .
.
Ces fonctions ![]() peuvent s'écrire
sous la forme
peuvent s'écrire
sous la forme ![]() , où
, où ![]() est définie par
est définie par ![]() .
.
Cette base est orthogonale, en effet on remarque que ![]() et
et ![]() . Il s'ensuit
que la base des
. Il s'ensuit
que la base des ![]() est orthogonale.
est orthogonale.
Les espaces Ep sont alors des espaces euclidiens. On
considère le supplémentaire orthogonal Fp de Ep dans Ep+1.
Ainsi on a ![]() pour tout p.
Cette décomposition sert à définir la tendance grossière d'un signal E0, et
ses détails à des résolutions de plus en plus fines (F0,F1,…).
pour tout p.
Cette décomposition sert à définir la tendance grossière d'un signal E0, et
ses détails à des résolutions de plus en plus fines (F0,F1,…).
2) algorithme de calcul des coefficients des ondelettes de Haar
L'ondelette mère de Haar est la fonction ![]() définie par :
définie par :
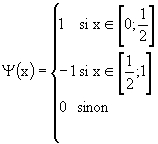 .
.
A partir de cette fonction, on définit les fonctions ![]() par
par ![]() .
.
De même que dans le paragraphe précédent, ![]() et
et ![]() car
car 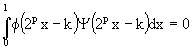 . On en déduit que la famille qui réunit les
. On en déduit que la famille qui réunit les ![]() et les
et les ![]() est une base orthogonale de
Ep+1, donc les
est une base orthogonale de
Ep+1, donc les ![]() forment une base
orthogonale de l'orthogonal Fp de Ep dans Ep+1.
forment une base
orthogonale de l'orthogonal Fp de Ep dans Ep+1.
Et on a le résultat fondamental suivant :
Pour tout ![]() , la famille
, la famille ![]() est une base orthogonale de Fp. De plus,
est une base orthogonale de Fp. De plus, ![]() .
.
Nous pouvons désormais calculer les coefficients d'ondelettes
associés à un signal ![]() . Il se décompose sous la
forme
. Il se décompose sous la
forme ![]() .
.
Puisque ![]() , sp se
décompose en
, sp se
décompose en ![]() avec
avec ![]() et
et ![]() .
.
Pour les mêmes raisons,
![]() et
et ![]()
et![]() et
et ![]() .
.
Ceci permet de déterminer facilement la décomposition de ![]() sur la base des
sur la base des ![]() et
et ![]() . En effet, si
. En effet, si ![]() alors l'orthogonalité de la base implique
alors l'orthogonalité de la base implique ![]() et
et ![]() . La décomposition
. La décomposition ![]() et les
valeurs des produits scalaires donnent alors
et les
valeurs des produits scalaires donnent alors ![]() et
et ![]() , d'où
, d'où ![]() et
et ![]()
L'intérêt est que l'on passe d'un échantillon de taille 2p à un échantillon principal de taille 2p-1 et un échantillon de taille 2p-1 en utilisant que des sommes ou des différences.
Si le signal est régulier, les valeurs des échantillons successifs
seront proches. Les coefficients de détails issus de la différence de deux valeurs
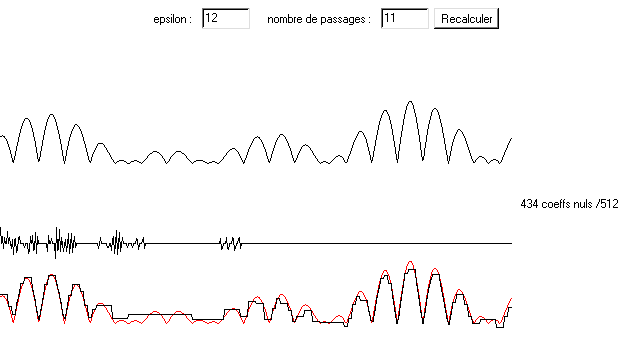
consécutives de l'échantillon seront donc petits. En s'imposant une précision ![]() , on ne gardera que les coefficients d'ondelettes
supérieurs en valeur absolue à
, on ne gardera que les coefficients d'ondelettes
supérieurs en valeur absolue à ![]() . Ceci permet une
compression du signal.
. Ceci permet une
compression du signal.
Voici l'algorithme utilisé : on reçoit un signal de la forme ![]() , on le décompose en
, on le décompose en ![]() et on transforme
et on transforme ![]() en
en ![]() ,
, ![]() avec
avec ![]() . On recommence ensuite le procédé avec le signal sp-1.
. On recommence ensuite le procédé avec le signal sp-1.
2) décomposition du signal sans pertes
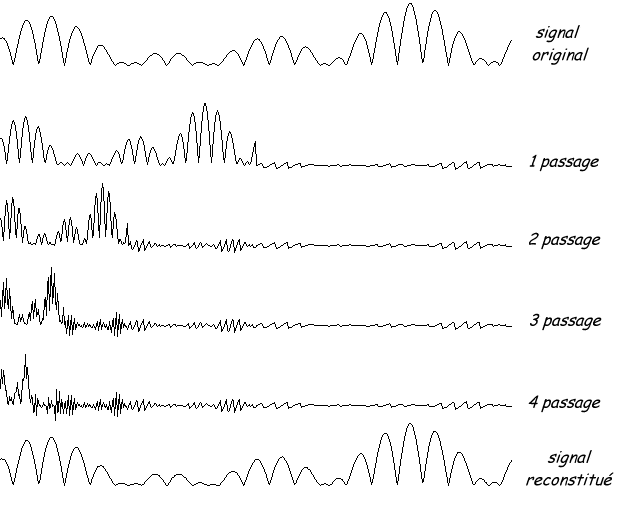
3) Décomposition d’un signal avec pertes
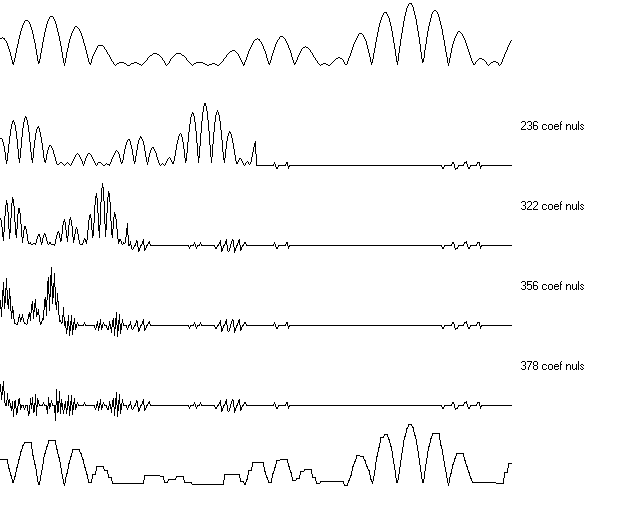
1) Présentation de l’algorithme
Une image en noir et blanc peut être considérée comme un ensemble de pixels, chaque pixel représentant un niveau de gris. On peut modéliser cette image par une matrice carré de taille égale à la résolution de l’image. Pour une image en couleur, il suffit de considérer trois images, chacune représentant le niveau de rouge, de vert et de bleu de l’image originale.
Pour mettre en application la méthode de Haar on pourrait considérer la matrice comme un échantillonnage en mettant ses lignes bout a bout. Cependant on perd le lien avec les colonnes. Il est donc plus efficace d’appliquer l’algorithme de Haar aux lignes de la matrice puis à ses colonnes. Cette algorithme de différentiation sommation se traduit par la multiplication matricielle à l’aide d’une matrice contenant beaucoup de 0.
Prenons l’exemple d’une matrice 4*4 :
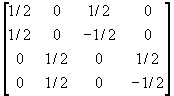
On l’appelle matrice A. en effet on remarque que si on prend une matrice M , soit (a,b,c,d) sa première ligne.. Alors le produit de M par A nous donne la ligne suivante.
![]()
Dans le cas d’une matrice 8*8 la matrice creuse aura l’allure suivante.
Soit A =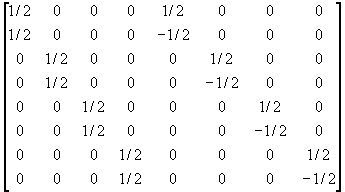
![]()
Et ainsi de suite, en fait c’est le principe déjà exposé dans la compression de signal, c’est à dire que la première moitié des colonnes de la matrice représente l’échantillon principal et la seconde les détails .
Quelque soit le rang de la matrice, on peut définir ses coefficients de la façon suivante :
Soit n le nombre de colonne de la matrice, n est pair, i et j des entiers positifs.
On a Ai,j =1/2 si j![]() n/2 et i=2j-1 ou 2j
n/2 et i=2j-1 ou 2j
On a Ai,j=1/2 si j>n/2 et i=2(j-n/2)
On a Ai,j=-1/2 si j>n/2 et i=2(j-n/2)-1
Sinon Ai,j=0
Ainsi quelque soit le rang de la matrice représentant l’image on peut facilement définir un algorithme et ainsi bâtir un programme permettant d’obtenir la matrice creuse de compression.
Pour effectuer l’opération sur les colonnes , il suffit de multiplier à gauche par la transposée de A. Nous obtenons donc une matrice N=t(A)MA
Ensuite on choisit une précision e , et on enlève de la matrice N les coefficients de valeur absolue inférieure a e. on obtient donc une nouvelle matrice N’. On réobtient la matrice M en posant M’=t(A-1)N’A-1 . A-1 étant la matrice inverse.
On peut reduire les calculs en rendant la Matrice orthogonal. Ainsi
l’inverse de la matrice A se calculera facilement. Les vecteurs de a sont déjà
orthogonaux par rapport au produit scalaire euclidien. Il suffit donc de les normés. Ici
il suffit donc de remplacer ½ par ![]()
On peut donc écrire la matrice A comme le produit de matrices orthogonales en prenant
Soit A1=
Soit A2
=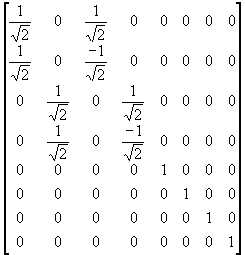

On a donc A=A1*A2*A3 , de ce fait on peut dire que A-1=tA1*tA2*tA3.
Compression

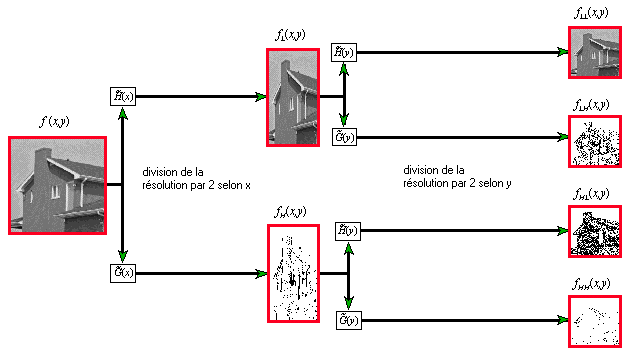
Décompression
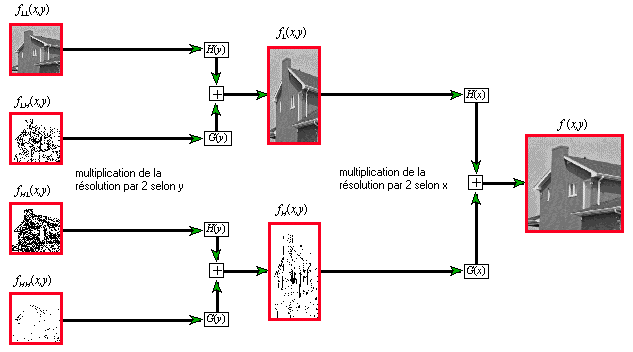
Les calculs se font facilement. Voici maintenant une application concrète de cette méthode.
3) Exemples d’images compressées par ondelettes
Le programme Compress que nous avons réalisé prend en entrée une image en format brut c’est à dire la suite des pixels qui composent les lignes de l’image. Chaque niveau de couleur est stocké sur un octets. En sortie le programme sort un fichier compressé selon la méthode LZW. Le programme decompress prend en entrée un fichier compressé par le programme compress et sort le fichier en format brut, on peut ainsi visualiser les pertes occasionnées par la compression par ondelettes.
L’utilisation des ondelettes de haar permet donc de nombreuses applications au niveau de la compression d’images et de signaux. D’autres familles d’ondelettes de Haar sont utilisées actuellement, elles offrent de meilleures résultat de compression. Elles sont suffisantes pour comprendre le principe de compression par ondelettes. L’algorithme que nous avons utilisé est plus performant que le standard JPEG, qui compresse la taille d’une image par 20 en moyenne alors que la méthode par ondelettes compresse en moyenne par 50.
Sur Internet